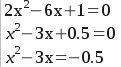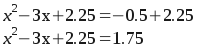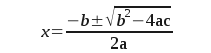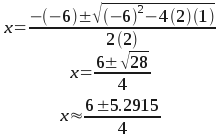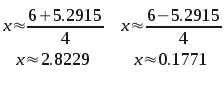Hi Daniel.

Completing the Square method:
To complete the square, what I do first is to get rid of the "a" term (the number at the front) by dividing it through both sides. Then I move the constant term to the other side (changing its sign en route). In your case, I then get this:

Now I complete the square by taking half the "b" term (that's the -3 in front of the x) and squaring that. Half of -3 is -1.5. Square that and I get +2.25. I add it to both sides.

At this point, I know the left hand side is a perfect square of the form (x - 1.5)^2. So I can take the square root of both sides, then I can solve for x. Note that when I take the square root, I take both the positive root and negative root, then solve them separately:

So the answers to the equation are x = {0.1771, 2.8229 }.

Quadratic Formula method:
With such problems, you also always have the option of using the Quadratic Formula. It looks like this:

In this form, "a" is the number in front of the x^2 term (if there is no number, it is implied to be 1) together with the sign. So in your example, a is 2. Similarly, b and c are the co-efficients of the x term and the constant term, with their signs. So b = -6 and c = 1.

So you can just put those numbers into the Quadratic Formula and simplify.

That "plus-or-minus" means there are two answers to the question. Here they are side by side. One is the plus version and the other is the minus version.

Cheers,
Stephen La Rocque