How fast is the length of his shadow changing?

HOME

Math Central

Quandaries & Queries

Question from Desiree, a student:

A spotlight on the ground shines on a wall 12 m away. If a man 2 m tall walks from the spotlight toward the building at a speed of 2.3 m/s, how fast is the length of his shadow on the building decreasing when he is 4 m from the building?

Desire,

As you know this is a related rates problem. You need to relate two rates, the rate at which the man is walking and the rate at which his shadow is decreasing. To do this I am going to find a relationship between the quantities that are changing and then differentiate with respect to time to develop a relationship between the rates at which they are changing.

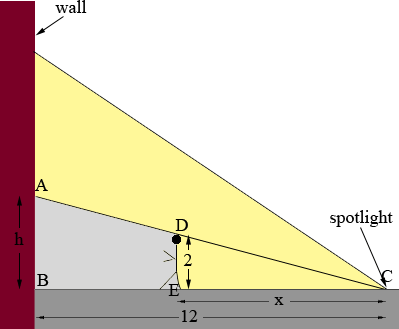
man, wall and shadow

I let x be the distance from the man to the spotlight in metres and h be the height of his shadow on the building, also in metres. These are the quantities that are changing and I want a relationship between them. For this I use the similar triangles ABC and DEC. Since they are similar

|AB|/|BC| = |DE|/|EC|

that is

h/12 = 2/x

hx = 24.

Both x and h depend on time t, measured in seconds, so differentiate this expression with respect to t to find a relationship between dx/dt and dh/dt. Evaluate this expression at x = 4 metres and solve for dh/dt at this time.

Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.