Donnie,

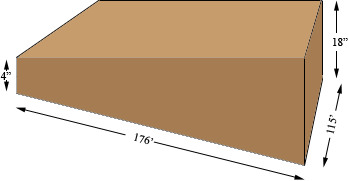
The volume is the area of the cross-section times te width of 115 feet. The shape of the cross-section is a trapezoid, a figure bounded by 4 lines, two of which are parallel. The area of a trapezoid is the average of the lengths of the parallel sides times the distance between the parallel sides. You have parallel sides of length 4 and 18 inches but you don't know the distance between them. It should be close to 176' but lets find it more exactly.

Before I begin I am going to change all the dimensions to yards since you asked for the volume in cubic yards. In yards the dimensions arre 176/3 = 58.67, 115/3 = 38.33, 18/36 = 0.50 and 4/36 = 0.11.

To find the distance between the parallel sides d I am going to use Pythagoras theorem.

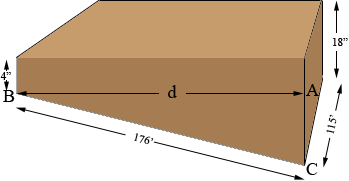
Triangle ABC is a right triangle |BC| = 58.67 yards, |CA| = 0.5 - 0.11 = 0.39 yards and |AB| = d yards. Thus

0.39² + d² = 58.67²

and hence

d = √(58.67² - 0.39²) = 58.67 yards.

Thus two 2 decimal places d and |BC| are the same length.

The area of the trapezoidal cross-section is thus

[(0.50 + 0.11)/2] × 58.67 = 17.89 square yards.

Finally the volume of fill you need is 17.89 × 38.33 = 686 cubic yards.

Harley