| |||
| Math Central | Quandaries & Queries |
|
Question from Ed: I am writing a science fiction novel that involves a spherical space station with a My problem is figuring out the total area of all of the floors, or for that I tried using trigonometry couldn't derive the radius of any floor but Floor 0. I would like the answers (total surface area of all floors and the number of Thanks. Ed |
Hi Ed,
In my diagram C is the centre of the sphere, B is the centre of some floor above C and A is a point on the circumference of this floor.
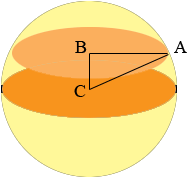
CA is a radius of the sphere so its length is 800 metres, the length of BC is the distance between the floors and AB is a radius of the floor. Once you know the length of AB you can find the floor area.
ABC is a right triangle so Pythagoras theorem gives us
|AB|2 + |BC|2 = |CA|2.
Hence
|AB| = √(8002 - |BC|2) metres.
Good luck with the novel,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.