| |||
| Math Central | Quandaries & Queries |
|
Question from Fausto, a student: i'm trying to figure out how many cubic yards i will need. I built a retaining wall that it's 5 feet high, running 90 feet long. There is a slope running to the wall of 24 degrees. The distance from the top of the slope to the wall is 12 feet. I don't know how to calculate how many cubic yards of fill dirt i need in there. Please help. Thanks! |
Fausto,
I tried to draw a diagram of the cross section.
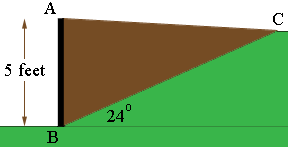
Is the diagram correct?
Is the distance from B to C 12 feet?
Harley
Fausto write back
Hello Harley,
Thanks for your reply. From the drawing i saw posted, the distance from A to C is 12 feet.
Fausto,
That makes the calculations particularly nice. If the angle CAB were a right angle then you can use Pythagoras theorem on the triangle ABC and conclude that BC has length 13 feet. This gives the slope angle as 22.37 degrees rather than 24 degrees but I think that will give a sufficiently accurate approximation of the volume of fill you need.
The volume of fill is the area of the triangle ACB times the length of the wall which is 90 feet. The area of the triangle is half the base times the height and since I am assuming the angle CAB is a right angle I can take the base to be AC and the height is then the length of AB. Thee measurements are all in feet and you want the volume in cubic yards so I am going to convert the lengths to yards by dividing each by 3.
Area of the triangle = (1/2) × (12/3) × (5/3) = 3.33 square feet.
Volume of fill = 3.33 × (90/3) = 100 cubic yards.
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.