Hi Gina,

I am going to solve this for a cubic tank that is 4 m on each edge and you can apply the same technique to a cubic tank that i 8 m on each edge.

I think of this as a big crate that is cubic and 4 m in each direction. I have a collection of cubical boxes that are 1 m on each side so each so each box has a volume of 1 cubic metre. I want to fill the crate with boxes to determine how many cubic metres I can fit in the crate. I start by putting 4 boxes on the crate, on the floor along the back wall.

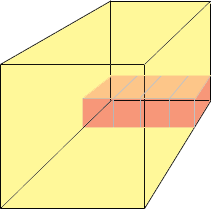
Now I put a second row of boxes on top of the first row, then a third on top of that and then a fourth. Four rows comes to the top of the crate so I have put in 4 × 4 = 16 boxes and I have completely covered the back wall.

Next I put 4 more boxes on the floor against the first four I put in place. I then put 3 more rows of 4 boxes on top of this to add another layer of 16 boxes. I can do this twice more so I have placed 4 × 16 = 64 cubic metre boxes in the crate. Thus the volume of the crate is 4 × 4 × 4 = 64 cubic metres.

Now try a cubical tank that is 8 m on each sid.

Penny