Heidi,

I think of a regular octagon as a square with the 4 corners lopped off.

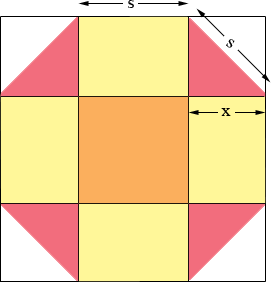
I let the length of the side of the octagon be s cm, chopped it up as in the diagram and introduced the variable x. The octagon is then partitioned into 9 regions

1 square of area s² cm²
4 rectangles each of area xs cm²
4 triangles

Two triangles can be put together along the hypotenuse to form a square which is x cm by x cm. Thus the total area of the regular octagon is

s² + 4 xs + 2 x² = 18 cm²

Each pink triangle is a right triangle with side lengths x, x and s cm. Thus by Pythagoras theorem

x² + x² = s²

Solve this equation for s, substitute into the equation for the area and solve for x. Once you have x you can use x² + x² = s² to find s.

Construct a square with side length s + 2x cm. Measure x cm in from each corner and cut off the corners. The resulting regular octagon has an area of 18 square centimeters.

Penny