| |||
| Math Central | Quandaries & Queries |
|
Question from Henry, a student: how many times does the graph of y=2xsquared -2x + 3 intersect the x-axis? |
Hi Henry,
I know that the graph of y = 2x2 -2x + 3 is a parabola and since the coefficient of x2 is positive (it's 2) the parabola opens upwards. Hence I know the graph looks like

The question is "Where is the X-axis?"
| Is the axis above the vertex so the graph intersects the x-axis twice and the equation 2x2 -2x + 3 = 0 has two real roots? | 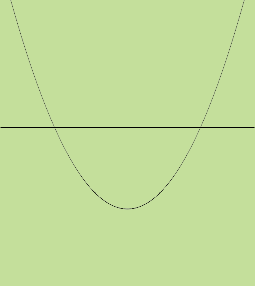 |
| Does the axis pass through the vertex so the graph intersects the x-axis once and the equation 2x2 -2x + 3 = 0 has one real root? | 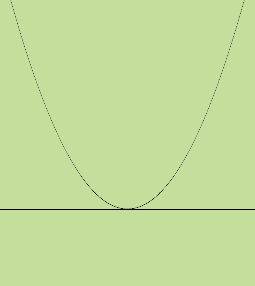 |
| Is the axis below the vertex so the graph does not intersect the x-axis and the equation 2x2 -2x + 3 = 0 has no real roots? | 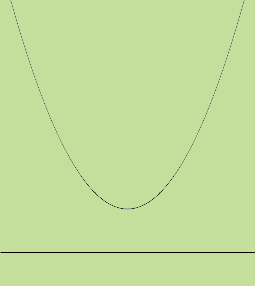 |
To decode which is the case solve the equation 2x2 -2x + 3 = 0, using the general quadratic if necessary, and decide how many real roots it has.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.