Ivan,

The area of the rectangular part is the width times the height so what remains to bee added is the area of the curved section.

I expect the curve is part of a circle so the area can be seen as

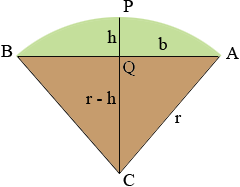
the area of the circle sector APBC minus the area of the triangle ABC. In my diagram Q is the midpoint of AB. Let h be the distance from Q to the top of the arch at P and b be the distance from A to Q.

First I need to find the radius of the circle r. Triangle AQC is a right triangle Pythagoras theorem gives us

b² + (r - h)² = r²

Simplifying and solving for r gives

r = (b² + h²)/(2h)                     (*)

Next I need the measure of the angle BCA. The tangent of the angle QCA is b/(r - h) and hence

angle BCA = 2 tan^-1[b/(r - h)]

The area of the sector APBC is a fraction of the area of the entire circle (π r²) and the angle BCA is a fraction of 360^o. By the symmetry these fractions are the same, that is

area(sector APBC)/ (π r² ) = (angle BCA)/360^o

and hence

area(sector APBC) = 2 π r² tan^-1[b/(r - h)]/360^o

The area of the triangle ABC is b(r - h) so finally

area of the transom APB = 2 π r² tan^-1[b/(r - h)]/360^o - b(r - h).                     (**)

Thus measure b and h, use expression (*) to find r and then use expression (**) to find the area.

I hope this helps,
Harley