Hi Jane,

This is an exercise with similar triangles.

Suppose A and B are points in the plane and you wish to determine the coordinates of M the midpoint of the line segment AB.

In the diagram below the line segment AC is parallel to the x-axis and the line segments CB and PM are parallel to the y-axis.

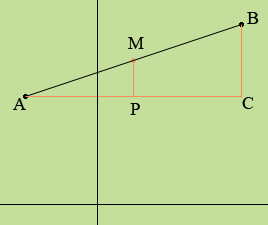
Triangles BAC and MAP are similar so

|BA|/|AC| = |MA|/|AP|.

But |BA| = 2|MA| so

2|MA|/|AC| = |MA|/|AP|

or

|AC| = 2|AP|.

Thus P is the midpoint of AC and hence the x-coordinate of P, which is also the x-coordinate of M, is the average of the x-coordinates of A and B.

A similar argument shows that the y-coordinate of M is the average of the y-coordinates of A and B.

For an example suppose A has coordinates (-2, 3) and B has coordinates (4, 5). The midpoint of the line segment AB then has x-coordinate (-2 + 4)/2 = 1 and y-coordinate (3 + 5)/2 = 4.

I hope this helps,
Penny