| |||
| Math Central | Quandaries & Queries |
|
Question from Jay, a student: Determine the area of the largest rectangle that can be inscribed between the x-axis and the curve defined by y = 26 - x^2. |
Hi Jay,
I inscribed a rectangle as you described. I let the x-coordinate where the rectangle touches the parabola be x and then the y-coordinate is 26 - x2.
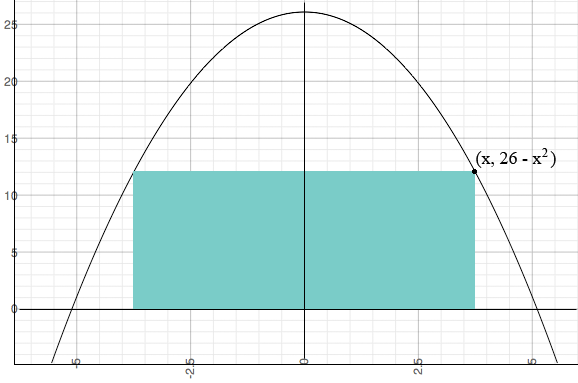
The area of the rectangle is A(x) = x × 2(26 - x2). Use the calculus you know to maximize A(x).
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.