| |||
| Math Central | Quandaries & Queries |
|
Question from Jeff: If I have a wedge shaped object (ie, a triangle of non-specific type extruded along a length) and it is sliced from the two-corner base at one end to the one-point tip at the other, what is the volume of the upper (smaller) part as a percentage of the whole? I hope I have explained it clearly enough. Thanks. |
Hi Jeff,
I am going to take the wedge and stand it on its end. The volume of the wedge is the area of the triangle ABC times the height of the wedge, h = |BE|.
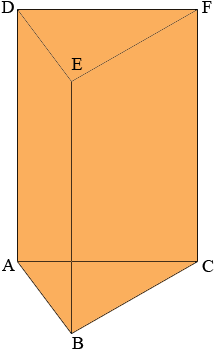
Next I slice from the line segment AC to the vertex E to form the solid figure ABCE that you described.
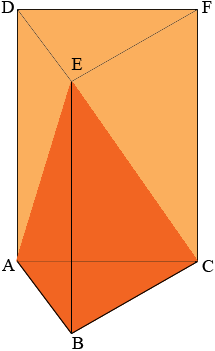
The solid figure ABCE can be described as follows. Take a triangle ABC in the plane and a point E not in the plane. Join each point on the perimeter of the triangle to the point E to form the boundary of solid ABCE. The volume of the solid ABCE can be found from a surprising geometric theorem.
If you take some region R in the plane with an area, some point V not in the plane and form a cone by joining every point on the boundary of R to V with a straight line then the volume of the cone is
(1/3) × (the area of the base) × (the height).
Thus the volume of the solid ABCE is (1/3) × (area of triangle ABC) × h. Hence the volume of ABCE is one third of the volume of the wedge.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.