Jeff,

Rather than trying to draw a diagram I just took a paper towel roll

cut it along the spiral seam and rolled it out flat. (there is a change of scale in the two photos.)

I then added some lines and labels.

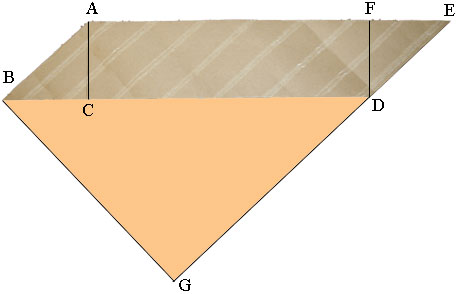
The side ED was extended to G so that angle BGD is a right angle. This makes the length |BG| equal to the height of the tube which I am going to call H. In your problem H = 102 inches.

Triangle ABC is a right triangle, |AC| = W is the width of the paper (in your example W = 3 inches) and |AB| = C is the circumference of the circular end of the roll (in your example C = π × diameter = 2π inches).

Triangle DBG is also a right triangle and since ED and AB are parallel angles ABC and GDB are congruent. Thus triangles ABC and DBG are similar. Hence

C/W = |BD|/H.

You know the values of C, W and H and hence you can find |BD|. The length of the paper strip required is |BD| + |EF|. But EF is the side of a right triangle with the hypotenuse of length C and the third side of length W and hence you can use Pythagoras theorem to find |EF|.

I hope this helps,
Penny