| |||
| Math Central | Quandaries & Queries |
|
Question from John, a parent: Hello: Probably a dumb question, but I couldn't find anything similar in your archives... My daughter wants to build an octagon using PVC pipe fittings. There are several pipe "elbows" available, including 45 degree. I'm trying to determine if if an octagon can be constructed by using 8 pairs of 45 degree elbows, connected to each other by 8 sections of straight pipe of some equal length. This makes sense to me intuitively, but I do not know how this can be properly expressed in geometric terms. Any help would be much appreciated!! thanks, John |
John,
The question is about the measure of the interior angles of a regular octagon (regular means all sides are of the same length).
If you draw a line from the centre of an octagon to each angle (8 lines in total), then each pair of consecutive lines makes an angle of 360/8 = 45 degrees. Each of the lines bisects one of the interior angles of the octagon (that is, divides it in half). This means that the triangles are all identical, and are the angles (or the triangle) adjacent to the side of the octagon are equal. Since the sum of the angles of a triangle is 180 degrees, each of them measures (180-45)/2 degrees. Since each interior angle of the octagon is comprised of two angles whose measure we just calculated above, each of them measures 180-45 = 135 degrees.
It looks as if elbow pieces that measure 45 degrees won't work.
Victoria
John,
I like this idea of maing an octagon from PVC pipe. Chris wrote back and suggested that you attach the pipe to the back side of one of its branches and the front side of the other.
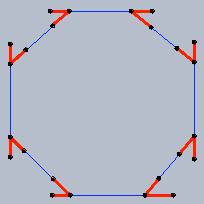
I don't see how to do this but are there 135 degree elbows among the parts you have available?
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.