Jonathan,

I have drawn what I see as your cone sleeve. Do I have the angle correct?

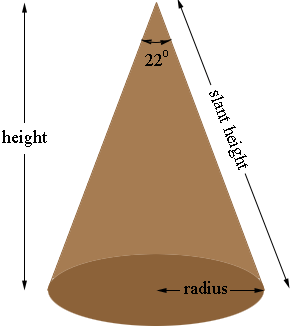
I need some additional information. Can you tell me the radius and either the height or the slant height?

Penny

Jon wrote back

The 22 degrees is correct however the slant height, radius and height will vary on the length of the sleeve i will make, but the 22 degrees is constant what I like to know is if i cut this conical sleeve, and place it flat on a table, what will be the angle, the degrees will change also sometimes I design a 25 degrees or 18 degrees cone sleeve, all I want to know what is the angle if i cut and place them flat on a a surface.

- Jon

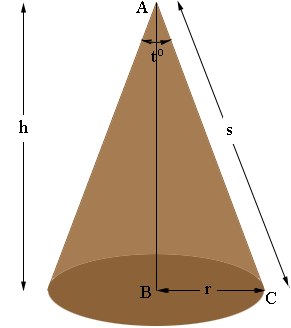
I redrew my diagram and labeled it. I changed the angle measurement from 22^o to t^o so that what I do applied to other sleeves as well.

The circumference of the circle at the base of the cone is 2 π r units.

When you slice the cone and roll it out flat you get a sector of a circle of radius s units and a central angle that measures w^o.

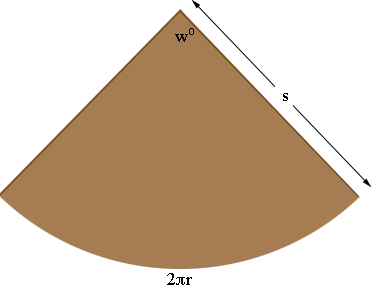
The circle of radius s has a circumference of 2 π s units and the arc of length 2 π r is a portion of that circumference just as w^o is a portion of the entire central angle of the circle of 360⁰. In fact by the symmetry of the circle these proportions are the same. That is

or

This give you the angle measurement you require from r and s. If you can't measure the radius of the base r or the slant height s directly you can calculate them using the trigonometric relations relating r, s and h.

r = h × tan(t/2)
h = s × cos(t/2)

r = s × sin(t/2).

I hope this helps,
Penny