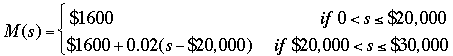| |||
| Math Central | Quandaries & Queries |
|
Question from Josh, a student: 1) A sales rep for a drug company is paid on the following scale. His base salary is $1600 per month. He is also paid a commission of 2% of sales over $20,000. When his gross sales reach $30,000 he is then paid 4% on the amount above that until his sales reach $50,000 after which point his commission becomes 6%. His commission reaches 8% when his sales total goes over $100,000 for the month. Set up a piecewise function for the information above. 2) How much would his gross salary be if his sales we: $112,000? |
Josh,
I can help get you started. In my mind I see the piecewise function as its graph so I am going to approach the problem graphically.
If his sales are $20,000 or less his salary is $1600 for the month.
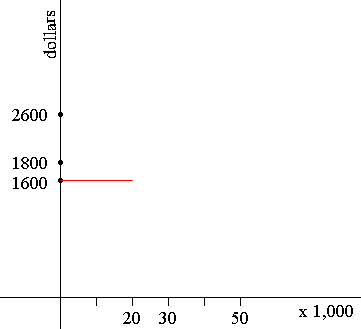
Salary in dollars against sales in thousands of dollars
If his sales are between $20,000 and $30,000 then his salary for the month increases in a linear fashion at 2% of sales over $20,000. Thus if he sells $30,000 worth of goods his salary will be
$16,000 + 0.02 × $10,000 = $1800.
Salary in dollars against sales in thousands of dollars
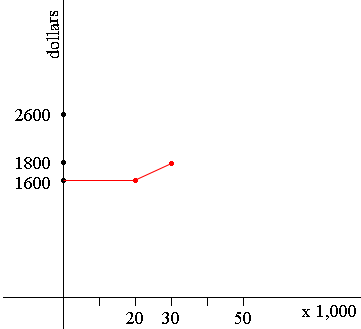
If his sales are between $30,000 and $50,000 then his salary for the month increases in a linear fashion at 4% of sales over $30,000. Thus if he sells $50,000 worth of goods his salary will be
$18,000 + 0.04 × $20,000 = $2600.
Salary in dollars against sales in thousands of dollars
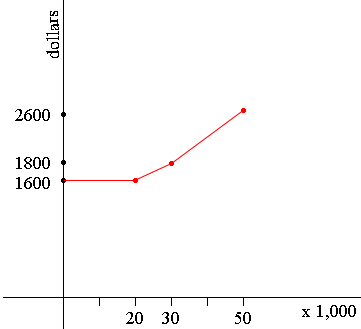
And so on.
But you want this in algebraic form so let s be his sales in dollars and M(s) be his salary for the month in dollars. You know that is s < $20,00 them M(s) = $1600.
If his sales are between $20,000 and $30,000, that is $20,000 < s ≤ $30,000 then he receives $1600 plus 2% of sales over $20,000, ie $1600 + 0.02(s - $2,000). Hence for sales up to $30,000 I get
Can you complete it now?
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.