Sigma in a normal distribution

HOME

Math Central

Quandaries & Queries

Question from Justin, a student:

Hello,

Here is the question:
Suppose the random variable Y can be described by a normal curve with Mu=40. For what value of the standard deviation is P(20 less than or equal to Y less than or equal to 60) = 0.50

I'm fairly certain the problem is actually solvable because we have the standard deviation. I just don't understand how to solve for it with the seemingly limited information in the problem. Solving for Z comes to mind, but there doesn't seem to be enough information. Thanks for your help!

-Justin

Hi Justin,

Changing the problem to a problem using the standard normal random variable Z is the right way to go. The conversion is which in your case is .

Your probability statement P(20 ≤ Y ≤ 60) = 0.50 can be represented graphically by

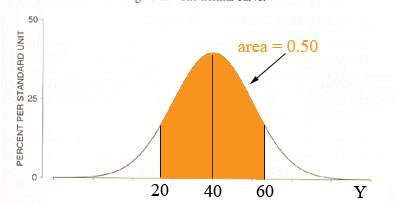
normal distribution

Notice that the shaded area is symmetric about the mean 40 so P(40 ≤ Y ≤ 60) = 0.25.

Now convert to the standard normal distribution and the diagram becomes

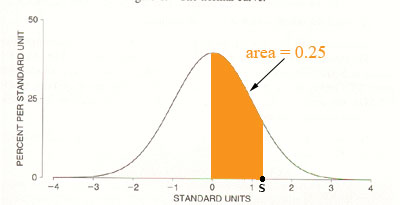
standard normal distribution

(I only brought across half of the shaded region because most of the standard normal tables I have seen make it easy to deal with areas between Z = 0 and Z = some positive number.) The point s on my diagram is the converted value for Y = 60, that is .

Use the normal table to determine the value of s, substitute into the equation above and solve for σ.

Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.