Hi,

Here is my vector diagram

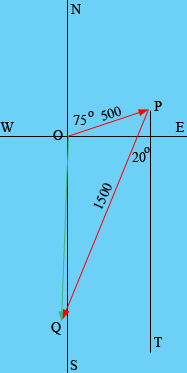
(It isn't drawn very accurately but it looks as if the resultant vector OQ is almost due south.) You can find the length of OQ with the law of cosines and the bearing of OQ with the help of the law of sines.

Try it, and if you need more assistance write back,
Penny

BF wrote

You showed katydid the graph of the two pairs: 500 at 75 degrees east of north
and 1500 at 20 degrees west of south.... but how do you work the problem out?
I don't get it, how do you use the law of cosines here?
(the answer is 1300 at 1 degree west of south according to the book)
I can't even get close to this...Thanks BF

BF,

The line PT is parallel to the north-south axis so the angle OPT has measure 75 degrees. This the angle OPQ has measure 75 - 20 = 55 degrees. Thus for the triangle OPQ you know the lengths of two sides and the measure of the angle between them and hence you can use the law of cosines to find the length of OQ.

Penny