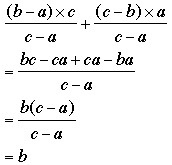A weighted average - Math Central

HOME

Math Central

Quandaries & Queries

Question from Kenneth:

Hello:

I am interested in determining the answers to the following question by using some type of weighted average:

An investor has $30,000 to invest at simple interest in two accounts. One account earns 2% and the second earns 5%. How much must he invest in each account if his total return is 4% or $1,200?

Here is a possible solution:
Let x = amount invested at 2% and 30,000-x is the amount invested at 5%. x = 10,000 is the amount invested at 2% and 30,000-10,000 = 20,000 is the amount invested at 5%.
10,000/30,000 = 1/3 and 20,000/30,000 = 2/3 these are the weights (1/3)(.02) + (2/3)(.05) = (0.12/3) = 0.04 = 4%

I want to determine the answers without using the above equation.

I discovered how to determine these fractions of 1/3 and 2/3 without first solving the equation:

2%----3%----4%----5%

From 2% to 5%, 2% is 2/3 of the distance to 4%. From 5% to 2%, 5% is 1/3 of the distance to 4%.
However, which fraction goes with which percentage, 2% and 5%, without using trial and error?
(2/3)(.02) + (1/3)(.05) does not equal 4%.

I thank you for your reply.

Kenneth,

In your example you know the weights are 1/3 and 2/3. Since 4% is closer to 5% than it is to 2% , 5% must get more weight than 2% and hence he must invest two-thirds of the $30,000 at 5% and the remaining one-third at 2%.

To see the general result suppose the percentages were a%, b% and c% with a < b < c. You found the weights as

(b - a)/(c - a) and (c - b)/(c - a).

The correct calculation is

since this is

Penny

Kenneth wrote back

I want to thank you for your reply. My mathematical level of thinking is not as advanced as I would like.
Can you explain in general terms why 5% must get more weight, 2/3?
5% is closer to 4%. It would seem reasonable that 2% should get more weight since it is farther from 4% to bring it closer to 4%.

I thank you for any helpful explanation that you can offer.

Kenneth,

The factors 2% and 5% are the interest rates of the two accounts. These values are fixed, you can't change them. The 4%, which you might call the effective interest rate, is determined by how much you have in the 5% account and how much you have in the 2% account. If all your money is in the 5% account then the effective rate is 5% and if all your money is in the 2% account then the effective rate is 2%. If you have half your money in each account then the effective rate will be half way between 2% and 5%, that is (2% + 5%)/2 = 3.5%. Since your effective rate is 4%, closer to 5% than to 2%, you must have had more money in the 5% account than in the 2% account. You already determined that the weights are 2/3 and 1/3 so you must have two-thirds of your money in the 5% account and one-third in the 2% account.

I hope this helps,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.