A maximum area problem - Math Central

HOME

Math Central

Quandaries & Queries

Question from Kylie, a student:

Help me please! I don't know how or where to start and how to finish.
The problem is: A window has the shape of a rectangle surmounted by a semicircle. If the perimeter of the window is 15 ft., find the dimensions that will allow the maximum amount of light to enter.

Kylie,

I can help get you started. I drew a diagram, labeled the width of the rectangle w, the height h and the radius of the semicircle r, all in feet.

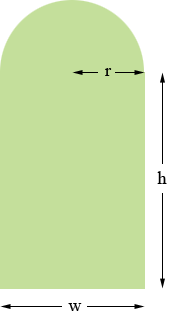
window

From the diagram w = 2r. Again from the diagram the perimeter is half the circumference of a circle of radius r plus the height of the rectangle twice plus the width of the rectangle once. You know the perimeter is 15 feet so

πr + 2h + w = πr + 2h + 2r = 15 feet.

Again using the diagram write an expression for the area of the window. Use w = 2r to write this expression as a function of r and h and then use the perimeter expression to write the area as a function of r alone. Now use the calculus you know to maximize this function.

Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.