Hi La,

I drew a diagram.

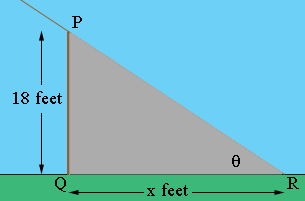
PQ is the flagpole and the ray RP points to the sun. The triangle PQR is in the shadow of the flagpole and |QR| = x feet is the length of the shadow on the ground. θ is the angle of elevation of the sun. θ and x are not constant, they are both functions of time t. Since you are going to need to differentiate to find the rate of change of θ you need to express it in radians rather than degrees.

Use a trig function to find a relationship between x and θ. Differentiate with respect to time t and substitute the values you have when θ is 45 degrees (π/4 radians) and solve for dx/dt.

Harley