La,

I know from one of your previous questions that you are studying calculus so I am going to treat this as a calculus problem.

I start with a sketch whenever possible.

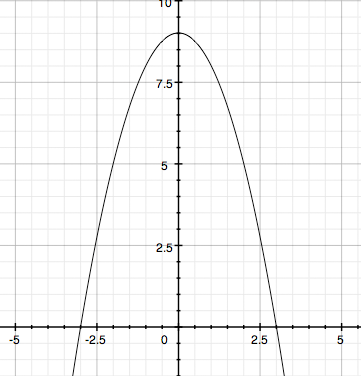
y = 9 - x²

Archimedes' formula for parabolic arches says that the area under the arch is 2/3 the base times the height. This parabola intersects the x-axis ay x = ± 3 and hence the length of the base is 2 × 3 = 6 units. The height is 9 units so using, Archimedes' formula, the area under the arch is 2/3 × 6 × 9 = 36 square units.

To verify that this result is true find the are using integration.

For a general parabolic arch modify the steps above for the expression y = a - bx².

Harley