Hi Liz,

I am going to try a smaller version of the problem.

if you had to match 3 players in the correct order for most popular outfielder from a pool of professional players labeled A through E , how many possibilities are there?

So I have 5 players named A through E and I need to order the three most popular.

I'm going to do this using a tree diagram. My tree starts at the root and has a trunk for each choice of the top ranked player. At the end of each trunk I write the name of the chosen player. No matter which trunk I choose to climb, when I reach the top I have 4 players to choose from for the second ranked player. I construct a branching at the top of each trunk for the four choices. (In my diagram I only drew 2 of the 5 branching at the second level.)

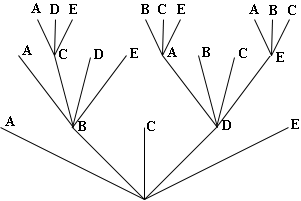
You can see that there are 5 × 4 = 20 paths from the root to the top of the second level in the tree. Thus there are 20 ways to produce a ranking of first and second. Again, no matter which path you have chosen to the top of the second level you have 3 choices for the player to rank third. At each position construct three branches to represent the choices. (This time I drew three of the 20 branchings at the top of the second level. Now you can see that there are 4 × 3 × 2 = 60 paths from the root to the top of the third level and thus 60 ways to produce a ranking of first, second and third.

Can you see how to extend this procedure to your problem?

Penny