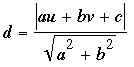Liza,

For this problem you should first know the formula that gives the distance from a point (u,v) to a line written in the form ax + by + c = 0: In the equation of the line, replace x by u and y by v, giving you some number. If that number is positive, call it n; if it is negative, then drop the minus sign and call the positive number n. Next, find the square root of a² + b² (where a and b are the coefficients of x and y in the equation of the line); call that number r. The distance from (u,v) to the line is then n/r. This formula is

For example, if the point is P = (1,2) and the line is 3x + 4y + 5 = 0,

n = 3 × 1 + 4 × 2 + 5 = 16;

r = sqrt(3²+ 4²) = sqrt(25) = 5.

The distance from P to 3x + 4y + 5 = 0 is therefore 16/5 (= 3.2).

In your problem the line is 5x + y - 13 = 0, and you are told that (u,v) is placed on the other line so that its distance from the first line is sqrt(26). That means you must find the unknown u and v by solving an equation. The fact that (u,v) is on the line 3x + y + 7 = 0 tells you that if you set u = x, then v = y = -3x - 7. So for n you have the positive value of 5x + (-3x - 7) - 13, and for r you have sqrt(5² + 1). Set the quotient n/r equal to the desired value of sqrt(26), and solve for x. That allows you to find y, which gives you the centre of your circle and, from that, the equation of your circle.

Chris