| |||
| Math Central | Quandaries & Queries |
|
Question from lyric, a student: tell whether the graph opens up or down. write an equation of the axis of symmetry |
Hi Lyric,
It really helps to have in your head the shape of the graph of a few simple functions and be able to build in them. For example I know that y = x is the straight line through the origin at a 45o angle an y = x2 is a parabola that open upwards with its vertex at the origin. I also know what the graph of y = 1/x looks like.
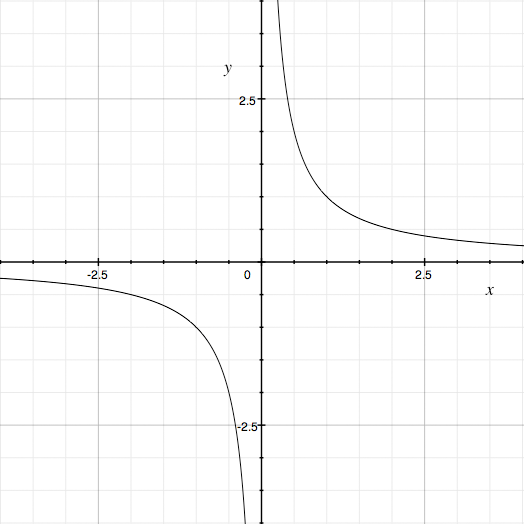
y = 1/x
Your function y = 4 x-4 = 4/x4 is similar in some ways, one being that the variable appears in the denominator. The 4 in the numerator is of little consequence as far as the shape of the graph is concerned, it just stretches the graph in the y-direction by a factor of 4. The fact that the denominator is x4 rather than x has a significant effect on the graph. If x is negative then y = 1/x is also negative so a piece of the graph lies below the X-axis. If x is either positive or negative y = 4/x4 is positive and hence the graph of y = 4/x4 lies entirely above the X-axis.
Can you see how to modify the graph of y = 1/x to obtain the graph of y = 4/x4?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.