Malysa,

I assume you mean a regular pentagon. I can get you started.

There is a point C in the pentagon that is equidistant from each of the 5 vertices. Join C to each of the 5 vertices and also to the midpoint of each edge.

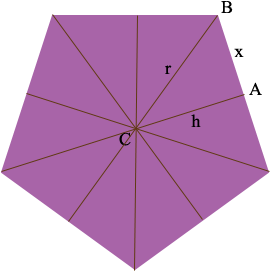
This subdivides the pentagon into10 congruent triangles. Look at one of the triangles, ABC in my diagram with side lengths r, h and x as in the diagram.

What is the measure of the angle BCA?

What is the formula for the area of the triangle? What is its value?

What trig function relates the two variables that appear in the formula for the area of the triangle?

If you need more help write back,
Harley