A normal distribution problem

HOME

Math Central

Quandaries & Queries

Question from Mark, a student:

hi,
I'm a college student and I have problem with this question..I'd appreciate if you could help me.

Final Averages are typically approximately normally distributed with a mean of 72 and a standard deviation of 12.5.
your professor says that the top 8% of the class will receive an A, the next 20%, a B, the next 42%, a C and the bottom 12%, an F.

a. What average must you exceed to obtain an A?
b. What Average must you exceed to receive a grade better than a C?
c. What average must you obtain to pass the course? (you'll need a D or better)

Thanks alot for your help, in advance.

Hi Mark,

You will need to convert the normal distribution you have to the standard normal distributable so that you can use the tables. The conversion from a normal random variable X with mean μ and standard deviation σ to the standard normal random variable is . For your distribution that's .

For part a) you want the number on the Z-axis that cuts off a tail to the right with an area of 8% or 0.08. This number is often designated Z_0.08.

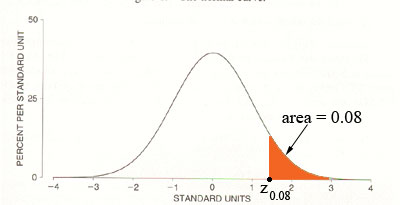
standard normal distribution

Use your normal table to find the value of Z_0.08. Set this number equal to and solve for X.

Parts b) and c) are similar.

Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.