| |||
| Math Central | Quandaries & Queries |
|
Question from mark: is there a simple way of finding out how much is left on a roll of paper. i have read similar questions and answers on here but all seem very complicated and not being very good at maths does not help me much. some are in inches and all have different figures to mine so if i give my figures hopefully i will understand it better. the radius of the cardboard core is 52.25mm, the radius of the paper at 2000 linear meters is 158.625mm. the thickness is 0.17mm. when nearing the end of the paper how do i work out how much is left in a simple way. thank you in advance for any help you can give me |
Hi Mark,
Can you check the measurements you sent? In particular is the paper thickness correct? The numbers just don't make sense to me.
Below is what I understand the roll looks like when there are 2,000 linear meters of paper on the roll. Is my diagram correct?
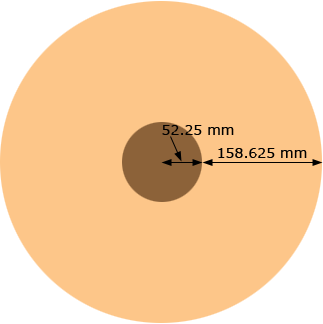
Harley
Mark wrote
yes harley my figures are correct. the core is 52.25mm, the radius of the paper at 2000 linear meters is 158.625, and the thickness of the paper is 0.17mm, or 120 gsm. your diagram is also correct. can you please give me an easy quick way of working out how much is left on the roll of paper with these figures, thanks again for your help
Mark,
I still have problems with the data you sent.
Look at the diagram above. The orange region, the edge of the rolled paper, is a region between two circles. The outside circle has a radius of 158.625 + 52.25 = 210.875 mm and the inside circle has a radius of 52.25 mm. The area of a circle is π time the square of the radius so the edge of the rolled paper has an area of
π × 210.8252 - π × 52.252 = 131,058 mm2
If you unroll the paper the edge forms a long, thin rectangle, 2000 m long by 0.17 mm high. 2000 m is 2000 × 1000 = 2,000,000 mm and thus the area of the edge of the paper is
2,000,000 × 0.17 = 340,000 mm2.
Thus one calculation of the area of the edge of the paper gives 131,058 mm2 and a second gives 340,000 mm2.
I can't give you a method to calculate the length of paper remaining on a partially used rool as I don't know what data to use.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.