Mary, I presume you want the minimum amount of box material (cardboard?). That's the surface area of the box. I'll also assume you double-up on material for flaps on the "open" ends. So we'd want the smallest end to be the open end.

Finally, I'll assume you want no air pockets for things to slip around. Intuitively we'd expect the smallest box to be one with no air pockets anyway.

Thus, we just look at the ways of stacking the boxes in rows. There are four possibilities:

A) 20 x 1 x 1
B) 10 x 2 x 1
C) 5 x 2 x 2
D) 5 x 4 x 1

Again, our mathematical intuition kicks in: we think that the box closest to a cube will be the best one, but those flaps muddy the waters...

For each of these possible arrangements, we have different orientations. Let's break them down:

A-1) 20x6cm; 1x36cm; 1x57cm
A-2) 20x36cm; 1x6cm; 1x57cm
A-3) 20x57cm; 1x6cm; 1x36cm (Crazy long box!)
B-1) 10x6cm; 2x36cm; 1x57cm
B-2) 10x6cm; 2x57cm; 1x36cm
B-3) 10x36cm; 2x6cm; 1x57cm
B-4) 10x36cm; 2x57cm; 1x6cm
B-5) 10x57cm; 2x36cm; 1x6cm
B-6) 10x57cm; 2x6cm; 1x36cm
C-1) 5x6cm; 2x36cm; 2x57cm
C-2) 5x36cm; 2x57cm; 2x6cm
C-3) 5x57cm; 2x6cm; 2x36cm
D-1) 5x6cm; 4x36cm; 1x57cm
D-2) 5x6cm; 4x57cm; 1x36cm
D-3) 5x36cm; 4x57cm; 1x6cm
D-4) 5x36cm; 4x6cm; 1x57cm
D-5) 5x57cm; 4x6cm; 1x36cm
D-6) 5x57cm; 5x36cm; 1x6cm (almost a pizza box)

Now for each of these 18 orientations, we would choose the side with the smallest surface area for the flaps (doubled-up material). So it helps to calculate the area of each side, then compute the total surface area of the material:

A-1) 20x6x1x36=4320; 20x6x1x57=6840; 1x36x1x57=2052. Therefore flaps also = 2520. Total surface area: 2(4320+6840+2052+2052)=30528.

A-2) 4320; 41040; 342. Flaps: 342. Total surface area: 91404.
A-3) 6840; 41040; 216. Flaps: 216. Total surface area: 96624.
B-1) 4320; 3420; 4104. Flaps: 3420. Total surface area: 30096.
B-2) 6840; 2160; 4104. Flaps: 2160. Total surface area: 30528.
B-3) 4320; 20520; 684. Flaps: 684. Total surface area: 52416.
B-4) 41040; 2160; 684. Flaps: 684. Total surface area: 89136.
B-5) 41040; 3420; 432. Flaps: 432. Total surface area: 90648.
B-6) 6840; 20520; 432. Flaps: 432. Total surface area: 56448.
C-1) 2160; 3420; 8208. Flaps: 2160. Total surface area: 31896.
C-2) 20520; 2160; 1368. Flaps: 1368. Total surface area: 50832.
C-3) 3420; 20520; 432. Flaps: 432. Total surface area: 49608.
D-1) 4320; 1710; 8208. Flaps: 1710. Total surface area: 31896.
D-2) 6840; 1080; 8208. Flaps: 1080. Total surface area: 34416.
D-3) 41040; 1080; 1368. Flaps: 1080. Total surface area: 89136.
D-4) 4320; 10260; 1368. Flaps: 1368. Total surface area: 34632.
D-5) 6840; 10260; 864. Flaps: 864. Total surface area: 37656.
D-6) 51300; 1710; 1080. Flaps: 1080. Total surface area: 110340.

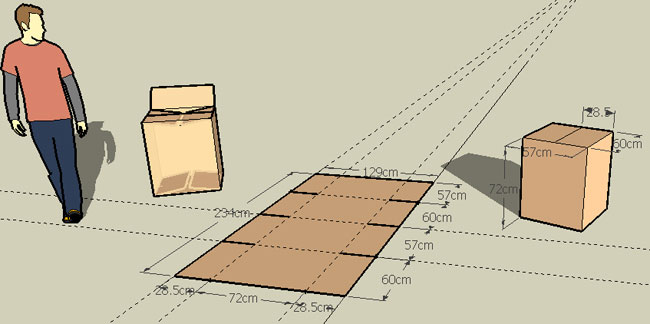
So looking at the list, B-1 is the smallest. So you can make your boxes 60cm x 72cm x 57cm, with the flaps on the 60x57 sides. This uses the least cardboard and packs all 20 items tightly into two rows of ten items.

I'd be tempted to shorten the inside flaps a bit and just go with 28.5 inch flaps all around. Thus, you can most easily cut from sheets of 234cm x 129cm. You might need to add a couple of cms on the wide side for seaming, too.

Stephen