| |||
| Math Central | Quandaries & Queries |
|
Question from Megan, a student: A plane flying with a constant speed of 330 km/h passes over a ground radar station at an altitude of 3 km and climbs at an angle of 30°. At what rate is the distance from the plane to the radar station increasing a minute later? |
Hi Megan,
Here is my diagram of your problem.
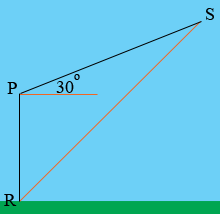
R is the position of the radar station, P is the position of the plane when it is directly above the station and S is the position of the plane t minutes later. You know that |RP| = 3 km, the measure of the angle SPR is 180o + 30o = 210o and the plane is flying at 330 km/hr which is 330/60 km/minute. Thus |PS| = (330/60) × t km.
Use the law of cosines to write an expression for |RS| as a function of t. Differentiate this expression to arrive at an expression for the rate at which |RS| is increasing and evaluate when t = 1 minute.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.