A sphere in a can of water

HOME

Math Central

Quandaries & Queries

Question from Meghan, a student:

Hi there,

I've got a (calculus) maximizing problem that I've been working at for a couple days now.
I can't figure out which variables to substitute in to get the desired answer.

A cylindrical can open at the top has (inside) base radius equal to 1.
The height of the can is greater than 2.
Imagine placing a steel sphere of radius less than 1 into the can, then pouring water into the can until the top of the sphere is just covered.

What should be the radius of the sphere so the volume of water used is as large as possible?

Thanks for your help in advance!
-Meghan

Meghan,

I let the radius of the sphere be r units and then, since the water just touches the top of the sphere, the height of the water is 2r units.

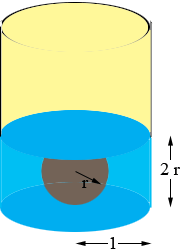
sphere in a cylinder

To determine the volume of water in the can find the volume of a cylinder of radius 1 unit and height 2r units and subtract the volume of a sphere of radius r units. This will give you a function of one variable r which you can maximize using your knowledge of calculus.

Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.