Hi Michael.

If you used a 24m rope, then certainly the goat has more than half the paddock.

A 24 x 24 square paddock has 576 square meters of area. Half that is 288 square meters. The goat's grazing area is a quarter-circle in shape. The area of a quarter circle is (1/4) π r². So we can just use the equation:

288 = (1/4) π r²

and solve for r:

(4/π)288 = r²
r² = 366.693
r = 19.15 m

The second part of the question is more difficult to work out. Basically, you have overlapping quarter-circles. But let's draw the diagonal from corner to corner as well, label the goats at A and C and the ends of the overlapping areas at B and D. Adding some additional lines we get the diagram below.

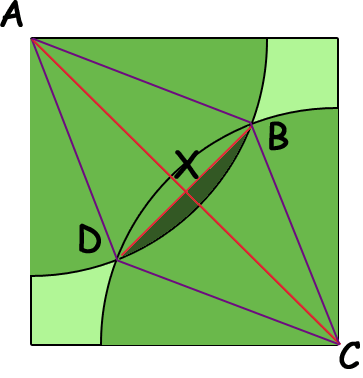
The area which the goats share is twice the area of the region in the diagram shaded dark green. The area of this dark green region is the difference between the area of the sector ADB and the area of the triangle ADB.

You can see that we have a rhombus ADCB of side length r with long diagonal AC. Since you know that the square has side length 24 m you can use Pythagoras theorem to find the length of the diagonal AC. Since X is the midpoint of AC and triangle AXB is a right triangle you can use trigonometry to find the measure of the angle BAX and thus the measure of the angle BAD. Knowledge of this angle and the length of AB allows you to find the area of the sector ADB.

All that remains is to find the area of the triangle ADB. You know its height AX so all you need is half its base XB which you can find using trigonometry or Pythagoras theorem.

Hope this helps,
Stephen La Rocque and Penny Nom