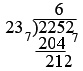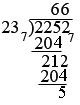Michelle,

I'm going to illustrate the procedure by dividing 821 by 17 in base 7. I am going to first convert 821 and 17, both written in base 10, to base 7. This procedure is illustrated in my response to an earlier question. Here is my conversion of 821 to base 7

821 ÷ 7 = 117, remainder of 2
117 ÷ 7 = 16, remainder 5
16 ÷ 7 = 2, remainder 2
2 ÷ 7 = 0, remainder 2

Thus 821 = 2252₇. Similarly 17 = 23₇.

Before I actually start the division I am going to calculate 1× 23₇, 2 × 23₇, 3× 23₇ 4× 23₇ 5× 23₇ and
6× 23₇ by repeated addition.

1 × 23₇ = 23₇
2 × 23₇ = 23₇ + 23₇ = 46₇
3 × 23₇ = 46₇ + 23₇ = 102₇

and so on. My resulting table is

1 × 23₇ = 23₇
2 × 23₇ = 46 ₇
3 × 23₇ = 102 ₇
4 × 23₇ = 125 ₇
5 × 23₇ = 151 ₇
6 × 23₇ = 204 ₇

Now I can start the division.

I can see from my multiplication that 23₇ divided 225₇. 6 times. Thus I get, after subtraction

Again using of the table I see that 23₇ divided 212₇ 6 times and thus

Thus 2252₇ divided by 23₇ is 66₇ with a remainder of 5₇ .

Penny