| |||
| Math Central | Quandaries & Queries |
|
Question from Olen: I work in a paper mill and have been handed the task to search for a formula to determine how much paper needs to be added to a parent roll to make up the difference at the winder. (Ex. The spool diameter at the reel is 18.25" we measure roughly 33.5" to make two 58" rolls in the winder. If the is a paper break and the roll diameter in the winder is 30" how much do I add to a single parent roll (22" roughly) to make one 58 " and the 28" needed at the winder. I would appreciate any help to complete this task. I would like to be able to build a chart that operators can refer to based on what is needed. Thank you. |
Olen,
I need some clarification. Are the rolls on the winder and the parent
roll all on spools with a diameter of 18.35 inches? I am having
trouble coming up with the 33.5 inches in your question.
Harley
Olen wrote back
I first want to thank you for your quick response, it is much appreciated.
I will start giving some known numbers from operators. At the reel, the parent roll that we make is on a reel spool 18.25 inches. The operators reel up to a size of 22 inches (measuring from the outside of the spool to the edge of the roll) to make a single roll at 58 inches in the winder, and 33.5 inches to make two 58 inch rolls at the winder. The core diameter used in the winder is 4.5 inches. I know that a calculation we tried will only give us the parent roll size if both rolls are equal size at the winder. When this calculation is done, we noticed it is a slightly smaller measurement than what we use. I believe that the main reason for that is because the parent roll at the reel is wound less tight than the roll in the winder.
This is what we are trying to achieve. If we experience a paper break that has enough paper on the reel spool to wind off, operators start a partial roll in the winder. Lets say that roll diameter is 30 inches with a 4.5 inch core. What we are trying to calculate is if I reel up a single at the 22 inch measurement from the edge of the reel spool to the edge of the roll, how much do I need to add to finish the 30 inch roll in the winder to a 58 inch roll.
What we would like to determine is would it be easy to formulate in a matter of a minute, or would we build a chart for let's say every quarter inch needed to complete the roll.
Once again I appreciate the time you are taking to look at this problem. Now I wish I would have paid more attention in algebra class.
Thank you,
Olen
Olen,
I drew what you described (not at all to scale) with all the units in inches.
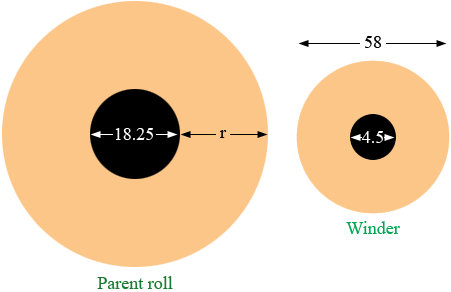
If the entire parent roll is wound onto the winder to produce 1 roll with diameter 58 inches then the areas shaded light orange in the diagram are equal. These are areas between two circles so on the winder the area is
π [(58/2)2 - (4.5/2)2] = 835.9375 π square inches.
On the parent roll the area is
π [(9.125 + r)2 - (9.125)2].
Hence π [(9.125 + r)2 - (9.125)2] = 835.9375 π which leads to the quadratic
r2 + 18.25 r - 835.9375 = 0.
Solving with the general quadratic gives r = 21.19 inches, very close to the 22 inches you are using.
If the parent roll is to produce 2, 58 inch diameter rolls at the winder then
π [(9.125 + r)2 - (9.125)2] = 2 × 835.9375 π
which leads to the quadratic
r2 + 18.25 r - 2 × 835.9375 = 0
which gives r = 32.77 inches, again close to 33.5 inches which you use.
Suppose now that there is a paper break and the roll on the winder has a diameter of d inches. If you reel up a single at the 21.19 inch measurement (you can use 22 if you wish) and then add a thickness of s inches as in the diagram the areas of the brown regions should be equal.
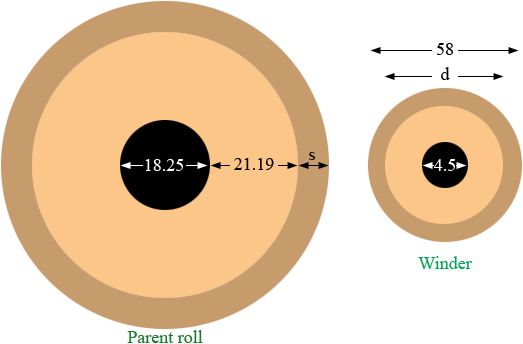
Thus
π[(9.125 + 21.19 + s)2 - (9.125 + 21.19)2] = π[(58/2)2 - (d/2)2]
This simplifies to
s2 + 60.630 s - 841 + (d/2)2 = 0
To construct your chart input values for d and solve the resulting quadratic for s. (you will obtain 2 values for s but one of them will be negative and hence extraneous.)
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.