Hi Paul,

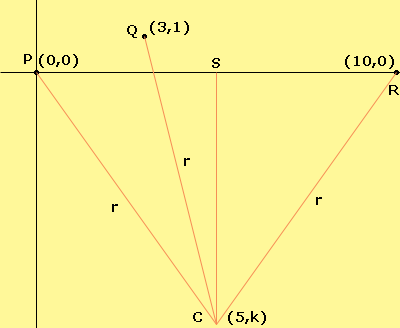
If C is the centre of the circle the C has coordinates (5, k) for some k. (From the diagram I know that k must be negative.) Triangle SPC is a right triangle and hence from Pythagoras theorem

r² = k² + 5².

Since Q is on the circle the distance from Q to C is r and hence the distance formula gives

r² = (5 - 3)² + (k - 1)²

Solve the two equations for k and then find r.

Harley

Paul, start by drawing the arc.

You will see that the center of the circle must lie on the vertical line x = 5, because that's half-way between points 1 and 3.

So we know the center point is (5, k) where k is the y value (clearly negative).

The equation of a circle with radius r and center at (h, k) is

(x - h)² + (y - k)² = r²

Thus, we know that the origin (point 1) is on the circle.  So we substitute in (0, 0) for (x, y) and we get this:

(0 - 5)² + (0 - k)² = r²
r² = k² + 25

As well, we know that (3, 1) is on the circle - that's point 2. So:

(3 - 5)² + (1 - k)² = r²
r² = k² - 2k + 1 + 4
r² = k² - 2k + 5

Now we can combine these two equations, because both right hand sides equal the same thing (r²):

k² + 25 = k² - 2k + 5
2k + 20 = 0
k = -10.

So the center is at (5, -10).  Use the distance formula to find the radius, then you will easily finish the problem.

Cheers,
Stephen La Rocque