| |||
| Math Central | Quandaries & Queries |
|
Question from Peter, a student: there is a competition problem where a cottage is worth 25000 years, but it decreases in value every year by 10 percent. Without a calculator, is there a way to find after how many years, the cottage will be worth 2500? (besides multiplying it out and besides logs) |
Sure Peter. As long as approximation is okay.
Just graph it, ideally using log paper. The situation boils down to (0.9)x = 0.1 Thus you can draw y = (0.9)x on logarithmic graph paper and look for the x value where it crosses y = 0.1.
So I just need one cycle semi-log paper. I know I start at 0.9. The next two are easy: 0.81 and 0.729. I plot these as X marks on the graph, then draw a straight line carefully through them (an exponential on log paper is drawn as a straight line).
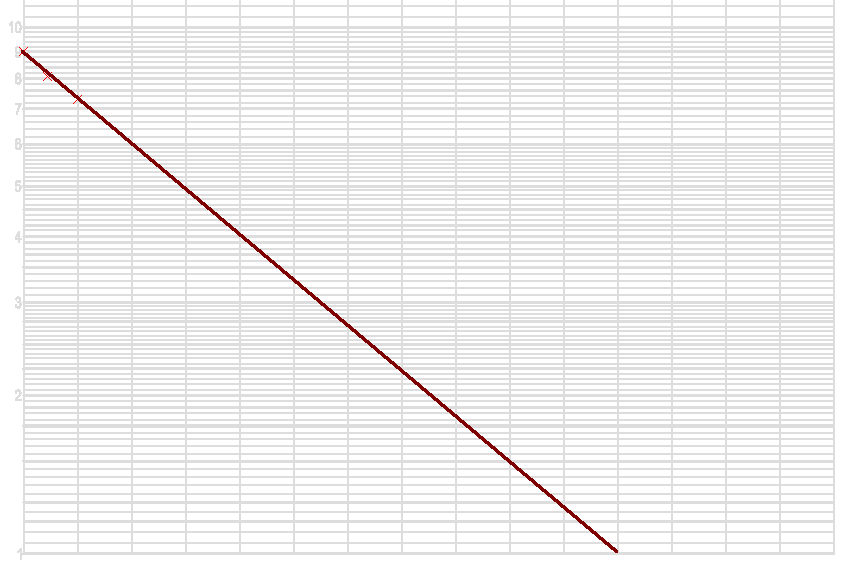
I see this crosses the 0.1 on the y axis at x = 22, so that means 22 years is the answer to the question. No repetitive calculations (indeed no calculator), no logarithms (except what's built into the graph paper) and a pretty good approximation.
In fact, using logs, I see that x = (log 0.1) / (log 0.9) = 21.85. Not bad.
Hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.