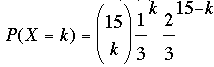A multiple choice exam - Math Central

HOME

Math Central

Quandaries & Queries

Question from Phalange, a student:

A multiple choice exam consists of 12 questions, each having 5 possible answers. To pass, you must answer at least 9 out of 12 questions correctly. What is the probability of passing if:
a. You go into the exam without knowing a thing, and have to resort to pure guessing?
b. You have studied enough so that on each question, 3 choices can be eliminated. But then you have to make a pure guess between the remaining 2 choices.
c. You have studied enough so that you know for sure the correct answer on 2 questions. For the remaining 10 questions you have to resort to pure guessing.

Phalange,

My exam has 15 question and I need to get 10 or more correct to pass. Each question has 3 possible answers and I haven't studied at all so I have to guess on each question. Thus for each question the probability that I get it right is 1/3.

You know this is a binomial distribution and hence if X is the number you get correct then

Hence to find the probability that I pass is P(X = 10) + P(X = 11) + ... + P(X = 15).

Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.