| |||
| Math Central | Quandaries & Queries |
|
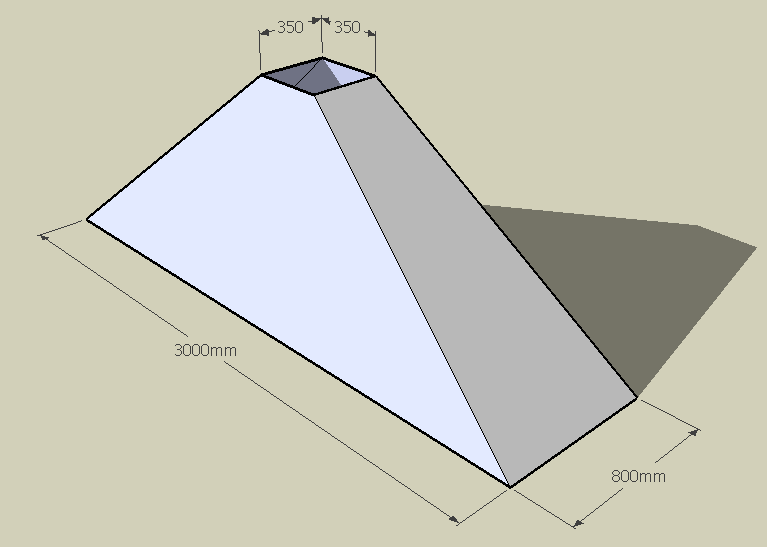
Question from phillip: Hi, I have a rectangular base to square top, pyramid shape to fabricate out of steel plate |
Hi Phil.
Is the sketch below what you are making?
Let me cut away the solid sides and show you some of the useful internal triangles that will solve this problem:
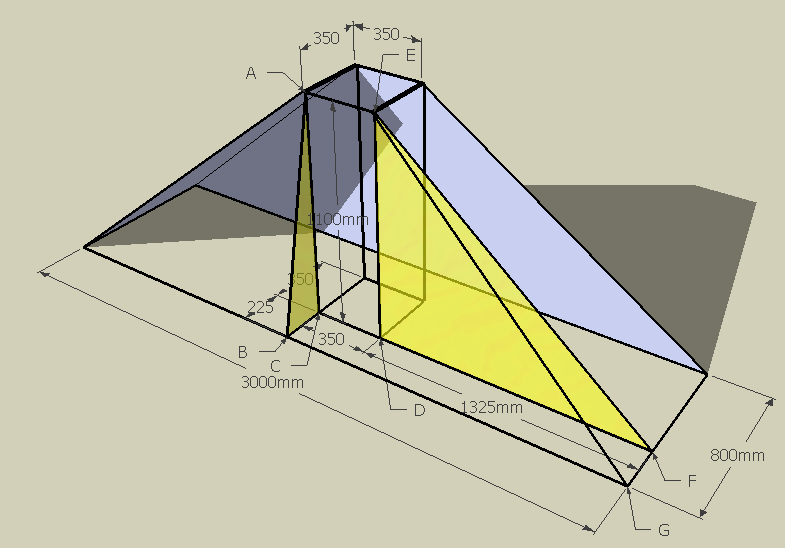
We can solve your question by using the Pythagoras' Theorem (a2 + b2 = h2). It relates the lengths of the sides of a right triangle to the length of its hypotenuse.
First consider triangle ABC. We know the length of AC is the height (1100) and the length of BC is 225
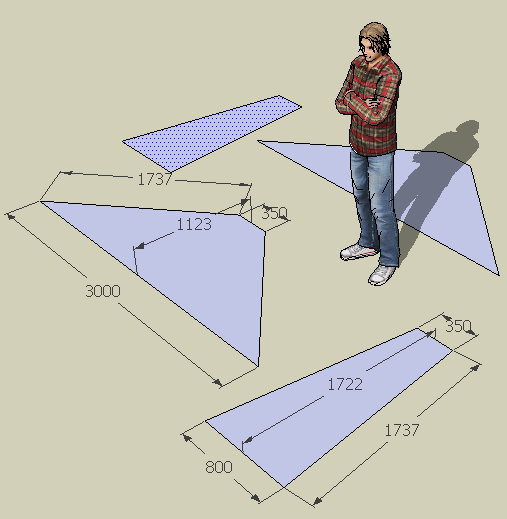
( (800-350)/2 ). So AB is the hypotenuse and it is sqrt(11002 + 2252) which is about 1123 mm. That is the "slant height" of the large pieces.
Now look at triangle DEF. We know ED is 1100 and DF is 1325 ( (3000 - 350) / 2 ). That makes the slant height of the narrow pieces (EF) equal to sqrt(13252 + 11002) which is about 1722 mm.
Finally, look at the triangle EFG. We know FG = 225 and (now) we know EF is 1722. So EG is sqrt(2252 + 17222) which is about 1737 mm.
Now we have all the measurements we need. Here are the two patterns we use for the four pieces:
Hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.