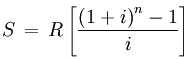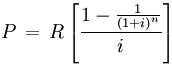| |||
| Math Central | Quandaries & Queries |
|
Question from Polly, a student: Susan contributed $500 every 6 months for 14 years into a RRSP earning interest @ 7.5% compounded semi-annually. Seven years after the last contribution Susan converted the RRSP into a RRIF which is to pay her equal 1/4 payments for 16 years. If the first payment is due 3 months after the conversion into the RRIF and the interest on the RRIF is 9% compounded 1/4, how much will Susan receive every 3 months? |
Hi Polly.
Break it into pieces.
Step 1: What is the value of the investment at the end of the 14 years of contributions?
You can use this formula to help:
where S is the value in 14 years, R is the payment size (500$), i is the interest per payment period (7.5% / 2 times each year = 0.0375) and n is the number of payments (14 x 2 = 28).
Step 2: What value does the RRSP grow to in the 7 years of dormancy?
You can use this formula to help:
A = P ( 1 + i )n
where A is the value after 7 years, P is the initial value (from step 1), i is the interest rate per compounding period (0.0375 again) and n is the number of compounding periods (7 times 2).
Step 3: Complete the problem by finding the quarterly payments needed to deplete the RRIF. A variant of the annuity formula from step 1 will do the job:
Where P is the principle (the value A from step 2), R is what you need to find (so you need to re-arrange the equation a little), i is the interest rate per period (9% per year in quarters equals 0.0225), n is the number of periods (16 x 4).
So solve for R and that's your answer.
For more explanation of how some of these equations come about, review my answer from yesterday here: http://mathcentral.uregina.ca/QQ/database/QQ.09.08/h/polly1.html and look up "compound interest" using our Quick Search.
Cheers,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.