| |||
| Math Central | Quandaries & Queries |
|
Question from prateet, a student: in an equilateral triangle prove that the centroid and centre of the circumcircle coincide here i am not clear about the concept of centroid and circumcircle |
Prateet,
You can look in our glossary for a definition of the centroid of a triangle and circumcentre of a triangle. You have an equilateral triangle and the symmetry in this triangle is very useful in working with the centroid and circumcircle.
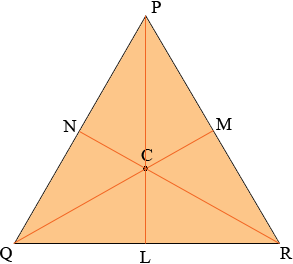
In my diagram L, M and N are the midpoints of the respective sides. C is the centroid. To show it in the circumcentre you need to show that |CP| = |CQ| = |CR|.
By the symmetry the line segment RN bisects the angle QRP. What is the measure of angle NRP? Again by the symmetry the 6 angles at C have the same measure. What is the measure of the angle MCR? What does this tell you about the triangle MCR?
Does this help?
If you need further assistance write back,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.