Hi Rachael,

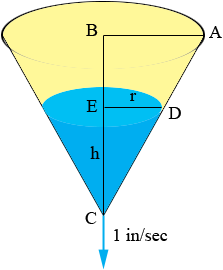
Let the radius and height of the water in the cone at time t seconds be r and h inches. The volume of the cone of water is then V = 1/3 π r² h cubic inches. V, h and r are all functions of time t. Triangles ABC and DEC are similar and |BC| is twice |AB| so h = 2r. You are told that dV/dt = -1 in³/sec and you want to find dh/dt at a particular time, the tie when |BE| = 2 inches. Use the fact that h = 2r (ie r = h/2) to express V as a function of h alone. Differentiate this expression implicitly with respect to t. This will result in an expression containing dV/dt, h and dh/dt. dV/dt and h you know at the time in question so you can solve for dh/dt.

Harley