Ray,

Draw a diagram.

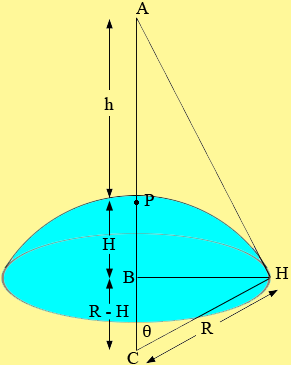
A is the airplane, P is the point on the surface of the Earth directly below the plane, h is the altitude of the plane, R is the radius of the earth, H is the point where the line of sight hits the horizon, C is the centre of the Earth and H is the height of the cap of the Earth which defines the visible surface region. The surface area is given by

S = 2 π R H.

Since R is a constant

dS/dt = 2 π R dH/dt.

What remains is to find dH/dt.

Triangle BCH is a right triangle. Use a trig function to write an expression relating R, H and θ. Use triangle ACH to write an expression relating R, h and θ. Solve these two expression to find a relationship relating R, H and h, and differentiate with respect to t.

Harley