Hi Rebecca.

I'll show you how to do this with a detailed example:

Example: Factor x² + 4x - 32 = 0.

To solve this question, I start by making a box that will reveal the answer.

I start by writing the "squared" term in the upper left and the last term (the constant term) in the lower right:

I am going to write the factors on the top and the left sides. This is just a table - you multiply the things at the top by the things on the left and put the product inside the corresponding box. First, I know that x² is just x times x:

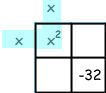
Now comes the hard part. I need to find two numbers that add to +4 (that comes from the +4x middle term) and that multiply to -32.

So I start by ignoring the minus sign for a moment and just think about what pairs of numbers multiply to make 32.
1 and 32 of course,
2 and 16, and
4 and 8.
Which pair is right? Well, it was a minus 32 and you know that only by multiplying a negative number by a positive number can you get a negative number. As well, I know that adding the numbers up, I have to get 4. If you can see quickly what it has to be, you can jump ahead.

I'll do it the long way so you can see. Each pair, I try switching the signs (one is positive and the other negative) and add them up. I'm hoping to add to 4.

-1 + 32 = 31 (nope)
1 + -32 = -31 (nope)
-2 + 16 = 14 (nope)
2 + -16 = -14 (nope)
-4 + 8 = 4 (yes!)

This means the two numbers I'm looking for are -4 and 8. I write them on the diagram. Note that where the column and row meet, I have -32, which is +8 times -4.

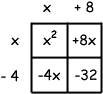
Now I can fill in the two empty spots. The row "x" times the column "+8" is +8x:

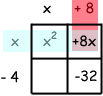
And the row "-4" times the column "x" is -4x:

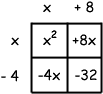
If you were to add up everything inside the four cells, you should get the original quadratic (once you simplify): x² + (+8x) + (-4x) + (-32) = x² + 4x - 32.

The box I worked with reveals the factors of the quadratic: they are the things outside the cells!

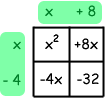
So the factors of x² + 4x - 32 are (x + 8) and (x - 4).

In other words, x² + 4x - 32 = (x + 8) (x - 4).

Try this method with your question, Rebecca. The trick will be to find a pair of numbers that multiplies to make +10 and that adds to make +7.

Hope this helps,
Stephen La Rocque