Hi Regina,

In an Euler diagram or Venn diagram is a collection of circles inside a rectangle that represents the universe of things under discussion. Suppose my universe is composed of wips, dips and pips then I would have three circles. One contains all the wips, circle W, one that contains all the dips, circle D, and one that contains all the pips, circle P.

In the most general situation their might be things that are both wips and pips, dips and not pips, wips, pips and dips or any other combination. Thus the most general position of the circles is

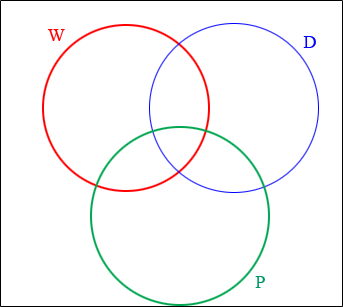
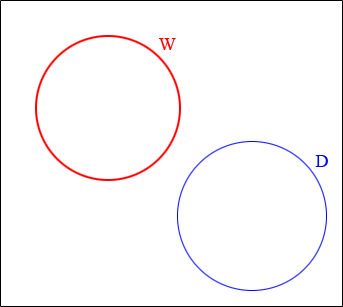
If you know that no wips are dips then there is no overlap of the W and D circles.

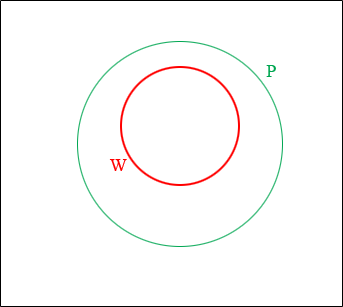
If all wips is a are pips then every wip must be inside the pip circle

Draw an Euler diagram that contains both requirements

No wizard can yodel
All lizards can yodel

What can you say about the wizard and lizard circles?

Penny