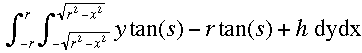 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Richard: I am trying to work at pouring angles and volume left in during pouring a crucible, The crucible is cylindrical and flat bottomed. I know the diameter, radius and volume of the crucibles. and the volume of liquid going into it. So lets say the crucible is only half full firstly I need to work out the angle just before its going to pour. ( I can work this out as long as there is a certain volume of liquid if its not enough I cant do it) Now the problem I also need to work out how much I should tilt the crucible to allow a certain amount out and be able to do this untill the volume reaches 0 at 90' turn. This is where I am stuck. The reason for needing to be able to work this out is so i can develop a constant flow for example 10Kg of metal per second. Thank you very much for you time |
Richard,
I drew the crucible upright to allow me to use the standard form of the mathematical expression for a cylinder. The radius of the crucible is r units and the height h units.
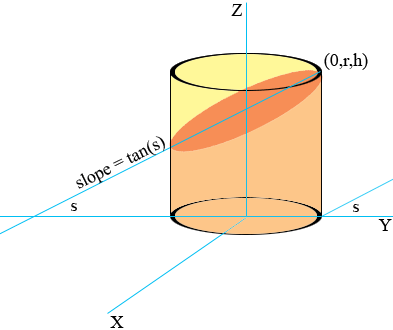
The plane that contains the surface of the liquid just before it is going to pour makes an angle of s degrees with the XY plane. A more natural angle fo you might be 90 - s degrees. The equation of this plane is
z = y tan(s) - r tan(s) + h
The volume of liguid in the crucible is the volume inside the cylinder and between this plane and the XY plane. This volume can then be found using a double integral,
volume
=
= π r2[h - r tan(s)] cubic units.
This expression is valid as long as the low side of the liquid surface meets the cylindrical side of the crucible, that is for 0 ≤ s ≤ tan-1(h/2r).
For tan-1(h/2r) ≤ s ≤ 90o the low side of the liquid surface meets the bottom of the crucible.
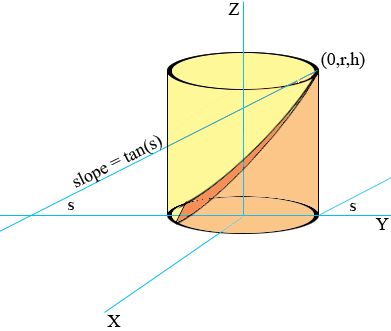
The volume of liquid in the crucible in this case is
volume
= 
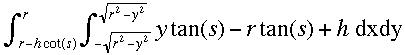
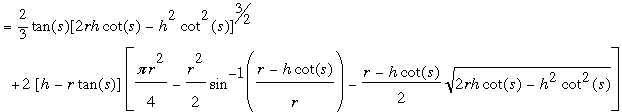cubic units.
This is not a particularly nice expression but for a specific crucible (known values of r and h) it is possible to construct a table that gives the volume for a range of values of the angle s.
Harley
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.