 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
I am trying to put landscape timbers down in octagon shape that measures 6 feet across and outside measures 360 degrees.. The timbers are 4 inches by 4 inches. I need to know at what angle to cut boards and at what length i need to complete octagon. I am a retired person with no previous math experience and am desperately need of this assistance. Thanking you in advance for your kind assistance. Richard :) |
Richard,
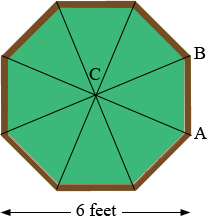
I joined the opposite vertices to subdivide the octagon into 8 triangles which all have a common vertex at the centre C of the octagon. The measure of the angle BCA is then 360o/8 = 45o. Triangle BCA is an isosceles triangle and hence angles ABC and CAB have the same measure (180o - 45o)/2 = 67.5o. This is the angle of the cut.
To calculate the side lengths I added to the diagram.
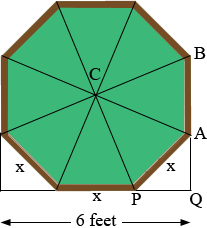
Suppose each side is x feet long. Triangle APQ is a right triangle so Pythagoras theorem tells us that the length of PQ is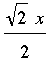 
feet. Hence 
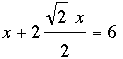. Thus
feet
which is 2 feet 5 13/16 inches.
I hope this helps,
Harley
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.