A garden in the shape of an isosceles triangle

HOME

Math Central

Quandaries & Queries

Question from Rita, a student:

Gregory wants to build a garden in the shape of an isosceles triangle with one of the congruent sides equal to 12 yards. If the area of his garden will be 55 square yards, find, to the nearest tenth of a degree, the three angles of the triangle.

My Work:

I had no idea how to solve this question. I know that it involves geometry. An isosceles triangle has two equal sides and one side that is different. I also know that the base angles of an isosceles triangles are equal. The formula to find the area of a triangle is A = (1/2)(bh).

I plugged 55 for area and got this equation:

55 = (1/2)(bh) but was not able to go forward because I don't know the base and height of this triangle.

What is the correct method for solving this question?

Rita,

You have one equation relating b and h, 1/2 (bh) = 55 and you need another so that you can use them to solve for b and h.

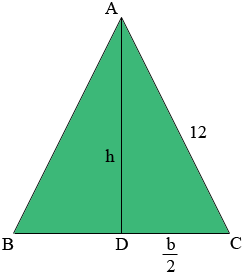
triangle

I called labeled the triangle ABC and let D be the midpoint of BC. ADC is a right triangle so by Pythagoras theorem

h² + (b/2)² = 12²

Solve for h in your first equation and substitute into the equation above and then solve for b.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.