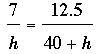| |||
| Math Central | Quandaries & Queries |
|
Question from robert: 12.5"@ base x 7" @ top and 40' height. How would I find the volume in cubic feet for a telephone pole with these dimensions? |
Robert,
I am going to assume that the 12.5" and 7" are diameters.
The pole is a truncated cone, a cone with the top cut off. If you extend the pole until it comes to a point and forms a cone then you can determine its volume by calculating the volume of the extended pole and then subtracting the volume cut off.
In my diagram I extended the pole to the point A and I let h feet be the height of the extension.
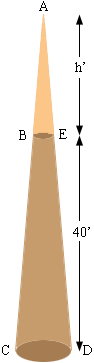
Since triangles ABE and ACD are similar
Solve this equation for h.
Use the fact that the volume of a cone is
1/3 π r2 h
to find the volume of the cone of height 40 + h feet and subtract the volume of the cone of height h feet.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.