Rogerson,

I graphed the function y = -x² - 6x - 5 for -2 ≤ x ≤ 4

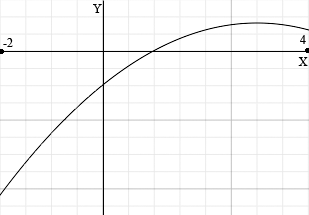
I then erased everything but the curve and the x-axis for 0 ≤ x ≤ 4.

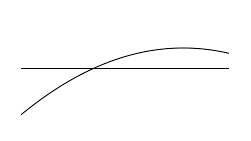
As you can see there is no finite region bounded by these two curves. Are you sure you have the question worded correctly?

Harley

Rogerson wrote back

Question from Rogerson, a student:

About my last question, yes I'm sure I worded it correctly. I even checked the problem and it is correct. in fact here is a similar question. If you can answer, thanks a lot.

Find the area, S, enclosed by the curve y = x^2 + 4x and the x-axis in the interval -1 ≤ x ≤ 4.

thanks a lot. please help, really need it :)

I think the question should say

Find the area, S, between the curve y = -x² + 6x - 5 and the x-axis in the interval 0≤x≤4.

I solved y = -x² + 6x - 5 and y = 0 to find that the curve intersects the x-axis at 1 nd 5. T then redrew my first diagram and shaded the region between the curve and the x-axis for 0 ≤ x ≤ 4

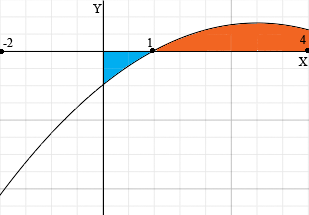
Part of the region is above the x-axis and part is below the x-axis. For the part above the x-axis, the part with 1 ≤ x ≤ 4, the area is

A similar integral from 0 to 1 will give a negative value since in that range the curve is below the x-axis. Hence you need to change the sign of the integral to obtain the area above the curve and below the x-axis. Thus the area, S, between the curve y = -x² + 6x - 5 and the x-axis in the interval 0≤x≤4 is

Evaluate this and try the second problem you sent. If you need further help write back.

Harley