Hi Sam,

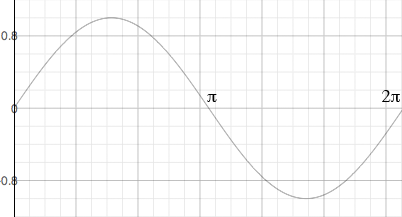
There are different ways to approach trig problems, I often think in terms of their graphs. I see the graph of y = sin(t) for t in [0, 2π], t in radians.

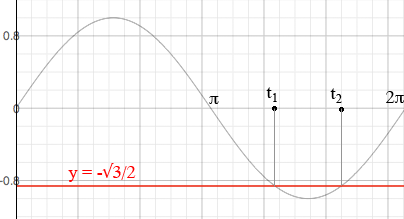
You have sin(t) = -√3/2 which is approximately -0.8399 so I get two values for t, t₁ and t₂.

I also know from the 1-2-√3 triangle that sin(π/3) = √3/2 and hence the distance labeled a in the diagram is π/3.

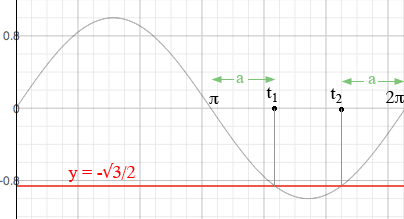
Hence t₁ = π + π/3 = 4π/3 and t₂ = 2π - π/3 = 5π/3. Since the sine is periodic with period 2π the solution to sin(t) = -√3/2 is t₁ plus or minus multiples of 2π and t₂ plus or minus multiples of 2π.

In your problem t = 4x so what solutions do you get for sin(4x) = -√3/2? Which ones are in [0, 2π]?

Harley